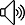Formulation
For non-negative integers? m ?and? n ?and a prime? p , the following? congruence relation ?holds:
where
and
are the base? p ?expansions of? m ?and? n ?respectively.
?
#include
<
iostream
>
#include
<
cstdio
>
#include
<
cstring
>
using
namespace
std;
typedef
long
long
llg;
const
int
N
=
150000
;
llg n, m, p, fac[N];
void
init()
{
int
i;
fac[
0
]
=
1
;
for
(i
=
1
; i
<=
p; i
++
)
fac[i]
=
fac[i
-
1
]
*
i
%
p;
}
llg pow(llg a, llg b)
{
llg tmp
=
a
%
p, ans
=
1
;
while
(b)
{
if
(b
&
1
) ans
=
ans
*
tmp
%
p;
tmp
=
tmp
*
tmp
%
p;
b
>>=
1
;
}
return
ans;
}
llg C(llg n, llg m)
{
if
(m
>
n)
return
0
;
return
fac[n]
*
pow(fac[m]
*
fac[n
-
m], p
-
2
)
%
p;
}
llg Lucas(llg n, llg m)
{
if
(m
==
0
)
return
1
;
else
return
(C(n
%
p, m
%
p)
*
Lucas(n
/
p, m
/
p))
%
p;
}
int
main()
{
int
t;
scanf(
"
%d
"
,
&
t);
while
(t
--
)
{
scanf(
"
%I64d%I64d%I64d
"
,
&
n,
&
m,
&
p);
init();
printf(
"
%I64d\n
"
, Lucas(n
+
m, n));
}
return
0
;
}
更多文章、技術交流、商務合作、聯系博主
微信掃碼或搜索:z360901061

微信掃一掃加我為好友
QQ號聯系: 360901061
您的支持是博主寫作最大的動力,如果您喜歡我的文章,感覺我的文章對您有幫助,請用微信掃描下面二維碼支持博主2元、5元、10元、20元等您想捐的金額吧,狠狠點擊下面給點支持吧,站長非常感激您!手機微信長按不能支付解決辦法:請將微信支付二維碼保存到相冊,切換到微信,然后點擊微信右上角掃一掃功能,選擇支付二維碼完成支付。
【本文對您有幫助就好】元