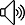上一篇博客介紹了神經(jīng)網(wǎng)絡其實就是兩步，第一步是前向傳輸，根據(jù)輸入的特征值與權(quán)重矩陣以及激活函數(shù)，不斷往前計算，得到輸出層的值，第二步就是后向傳播，根據(jù)殘差的加權(quán)求和，不斷往后，直到輸入層，然后更新權(quán)重，不斷進行這兩步，直接輸出結(jié)果的誤差在所要求范圍內(nèi)即可 。

本篇博文通過python代碼實現(xiàn)神經(jīng)網(wǎng)絡，采用sklearn自帶的手寫數(shù)字集，看分類情況如何

一、導入數(shù)據(jù)集并標準化
數(shù)據(jù)集的加載非常簡單，直接調(diào)用load_digits即可，常用到的數(shù)據(jù)有：
digits.data：手寫數(shù)字特征向量數(shù)據(jù)集，每一個元素都是一個64維的特征向量。
digits.target：特征向量對應的標記，每一個元素都是自然是0-9的數(shù)字。
digits.images：對應著data中的數(shù)據(jù)，每一個元素都是8*8的二維數(shù)組，其元素代表的是灰度值，轉(zhuǎn)化為以為是便是特征向量

            
              # python實現(xiàn)神經(jīng)網(wǎng)絡
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import seaborn as sns

#導入數(shù)據(jù)集（dataset自帶的手寫數(shù)字數(shù)據(jù)集)
data = load_digits()
print(data.images.shape)
X = data.data
Y = data.target
print(X.shape,X[:2])
print(Y.shape,Y[:2])
 stander = StandardScaler() # 特征值進行標準化，得到均值為0，方差為1的分布
 X = stander.fit_transform(X)
 print(np.unique(Y,return_counts=True))  # 輸出每一種類別及類別的數(shù)量

            
          

二、數(shù)據(jù)拆分

將數(shù)據(jù)拆分成80%的訓練集和20%的測試集

            
              X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.2)
print(X_train.shape)
print(Y_train.shape,Y_train)
print(Y_test.shape)

            
          

三、創(chuàng)建神經(jīng)網(wǎng)絡

            
              V = np.random.random((64, 100))*2-1 # 輸入層到隱藏層的權(quán)重矩陣，范圍0~1
W = np.random.random((100,10))*2-1  # 隱藏層到輸出層的權(quán)重矩陣，范圍0~1

# 激活函數(shù)sigmoid函數(shù)
def sigmond(x):
    return 1/(1+ np.exp(-x))

# sigmoid函數(shù)的導數(shù)
def sigmondf(x):
    return x*(1-x)

# 預測函數(shù)
def predict(x):
    L1 = sigmond(np.dot(x, V))
    L2 = sigmond(np.dot(L1, W))
    return L2

# 神經(jīng)網(wǎng)絡分類器
def network(X, Y, steps=10000):
    global W,V  # 定義全局變量
    acc_list = []
    for lt in list(np.linspace(0.001,0.01,100)):
        acc_0 = 0
        for n in range(steps+1):
            i = np.random.randint(X.shape[0])
            X = X[i]  # 這是一個一維的矩陣，（64，）
            X = np.atleast_2d(X)  # atlease_xd變成幾維，如果是2,則是2維，如果是3，就變成3維，[]，[[]],[[[]]]
            L1 = sigmond(np.dot(X,V)) # 得到一個（1，100）的矩陣
            L2 = sigmond(np.dot(L1,W)) # 得到一個（1，10）的矩陣
            L2_delta = (Y[i] - L2)*sigmondf(L2)  # 輸出節(jié)點的殘差： -（輸出值-樣本值）* 激活函數(shù)導數(shù) （1，10）
            L1_delta = np.dot(L2_delta,W.T)*sigmondf(L1)  # 隱藏層的殘差：右側(cè)輸出層的殘差加權(quán)求和*隱藏層的導數(shù) （1，10）（10，100）=（1，100）
            W += lt*np.dot(L1.T,L2_delta) # 隱藏層更新權(quán)重：(100,1)*(1,10)=(100,10)
            V += lt*np.dot(X.T,L1_delta)  # 輸入層更新權(quán)重：(64,1)*(1,100)=(64,100)
            if n%1000 == 0:  # 取余，如果迭代達到1000的倍數(shù)
                predict_ = predict(X_test)
                predictions = np.argmax(predict_, axis=1) # 每一行最大值的下標,對于多分類，輸出值最大的即為分類結(jié)果
                acc = np.mean(np.equal(predictions, Y_test)) # np.equal是判斷是否相等，相等的變?yōu)門rue，不相等的就變?yōu)镕alse,然后計算均值
                if acc>acc_0:
                    acc_0 = acc
                # print('第{}次'.format(n)+'      '+ '平均準確率:', acc)
        acc_list.append(acc_0)
    return acc_list
    
acc_list = network(X_train,Y_train)
plt.plot(np.linspace(0.001,0.1,100),acc_list)
plt.show()

            
          

跑出來準確率不高，于是不斷替換學習率，發(fā)現(xiàn)最高的也僅能達到13%，嘗試對初始權(quán)重進行調(diào)整，也沒有太大的變化，不過本篇主要的目的就是想用python實現(xiàn)神經(jīng)網(wǎng)絡，對于分類的準確度倒在其次，后續(xù)打算會用sklearn庫封裝的神經(jīng)網(wǎng)絡試試看。